Integral


Integration is the reverse operation of derivation.

The Integral of a function is the area under the function's graph.

Indefinite Integral Definition

When dF(x)/dx = f(x) => integral(f(x)*dx) = F(x) + c

Indefinite Integral Properties

integral(f(x)+g(x))*dx = integral(f(x)*dx) + integral(g(x)*dx)

integral(a*f(x)*dx) = a*integral(f(x)*dx)

integral(f(a*x)*dx) = 1/a * F(a*x)+c

integral(f(x+b)*dx) = F(x+b)+c

integral(f(a*x+b)*dx) = 1/a * F(a*x+b) + c

integral(df(x)/dx * dx) = f(x)

Change of Integration Variable

When x = g(t)  and dx = g'(t)*dt

integral(f(x)*dx) = integral(f(g(t))*g'(t)*dt)

Integration By Parts

integral(f(x)*g'(x)*dx) = f(x)*g(x) - integral(f'(x)*g(x)*dx)

Integrals Table

integral(f(x)*dx = F(x) + c

integral(a*dx) = a*x+c

integral(x^n*dx) = 1/(a+1) * x^(a+1) + c , when a<>-1

integral(1/x*dx) = ln(abs(x)) + c

integral(e^x*dx) = e^x + c

integral(a^x*dx) = a^x / ln(x) + c

integral(ln(x)*dx) = x*ln(x) - x + c

integral(sin(x)*dx) = -cos(x) + c

integral(cos(x)*dx) = sin(x) + c

integral(tan(x)*dx) = -ln(abs(cos(x))) + c

integral(arcsin(x)*dx) = x*arcsin(x) + sqrt(1-x^2) + c

integral(arccos(x)*dx) = x*arccos(x) - sqrt(1-x^2) + c

integral(arctan(x)*dx) = x*arctan(x) - 1/2*ln(1+x^2) + c

integral(dx/(ax+b)) = 1/a*ln(abs(a*x+b)) + c

integral(1/sqrt(a^2-x^2)*dx) = arcsin(x/a) + c

integral(1/sqrt(x^2 +- a^2)*dx) = ln(abs(x + sqrt(x^2 +- a^2)) + c

integral(x*sqrt(x^2-a^2)*dx) = 1/(a*arccos(x/a)) + c

integral(1/(a^2+x^2)*dx) = 1/a*arctan(x/a) + c

integral(1/(a^2-x^2)*dx) = 1/2a*ln(abs(((a+x)/(a-x))) + c

integral(sinh(x)*dx) = cosh(x) + c

integral(cosh(x)*dx) = sinh(x) + c

integral(tanh(x)*dx) = ln(cosh(x)) + c

 

Definite Integral Definition

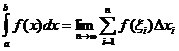
integral(a..b, f(x)*dx) = lim(n->inf, sum(i=1..n, f(z(i))*dx(i)))  

When x0=a, xn=b

dx(k) = x(k) - x(k-1)

x(k-1) <= z(k) <=x(k)

Definite Integral Calculation

When  ,

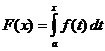  dF(x)/dx = f(x)  and

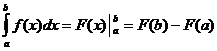
integral(a..b, f(x)*dx) = F(b) - F(a)  

Definite Integral Properties

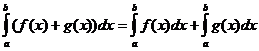
integral(a..b, (f(x)+g(x))*dx) = integral(a..b, f(x)*dx) + integral(a..b, g(x)*dx)

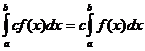
integral(a..b, c*f(x)*dx) = c*integral(a..b, f(x)*dx)

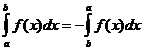
integral(a..b, f(x)*dx) = - integral(b..a, f(x)*dx)

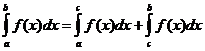
integral(a..b, f(x)*dx) = integral(a..c, f(x)*dx) + integral(c..b, f(x)*dx)

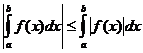
abs( integral(a..b, f(x)*dx) ) <= integral(a..b, abs(f(x))*dx)

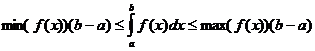min(f(x))*(b-a) <= integral(a..b, f(x)*dx) <= max(f(x))*(b-a)  when x member of [a,b]

Change of Integration Variable

When x = g(t)  , dx = g'(t)*dt  , g(alpha) = a  , g(beta) = b

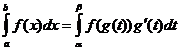
integral(a..b, f(x)*dx) = integral(alpha..beta, f(g(t))*g'(t)*dt)

Integration By Parts

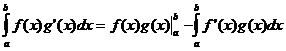
integral(a..b, f(x)*g'(x)*dx) = integral(a..b, f(x)*g(x)*dx) - integral(a..b, f'(x)*g(x)*dx)

Mean value theorem

When f(x) is continuous there is a point c is member of [a,b]  so

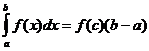
integral(a..b, f(x)*dx) = f(c)*(b-a)   

Trapezoidal Approximation of Definite Integral

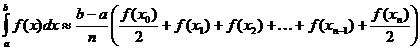
integral(a..b, f(x)*dx) ~ (b-a)/n * (f(x(0))/2 + f(x(1)) + f(x(2)) +...+ f(x(n-1)) + f(x(n))/2)

The Gamma Function

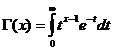
gamma(x) = integral(0..inf, t^(x-1)*e^(-t)*dt

The Gamma function is convergent for x>0.

Gamma Function Properties

G(x+1) = xG(x)

G(n+1) = n! , when n is member of ℕ (positive integer).

The Beta Function

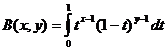
B(x,y) = integral(0..1, t^(n-1)*(1-t)^(y-1)*dt

Beta Function and Gamma Function Relation

B(x,y) = Gamma(x)*Gamma(y)/Gamma(x+y)

 


 

 

CALCULUS
CONTACT